



ARM code for Beginners
Part 7: Using BASIC arrays
Brain Pickard explains how anyone can program in ARM code.
Last time I explained how the BASIC CALL command can pass values stored in BASIC variables. In this part I will extend these ideas to included arrays.
The solutions to the problems sets in part 6 are on the CD they are called soln1 and soln2.
BASIC arrays can be integer, real or string, and are used in the CALL command by giving their name followed by () thus:
CALL code%, a%(), a(), a$()
They can be of any number of dimensions. They have type 256+4, 256+5 and 256+128 which are the same types as the single value parameters but with bit 8 set. In all cases the address word held in R9 points to a word aligned word for the array called the Subscript list as shown below.
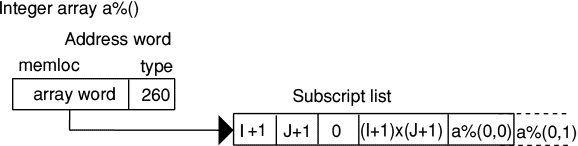
Note the BASIC DIM command actually produces arrays which start with indices zero up to the value in the DIM. DIM a%(1,4) produces 10 elements a%(0,0) up to a%(1,4).
The first word of the subscript list holds the number of elements of the first dimension, the second the number of elements of the second dimension and so on for all the dimensions, the list ending with a zero word. The next word holds the total number of elements of the array. This is followed by words containing the values of each element of the array.
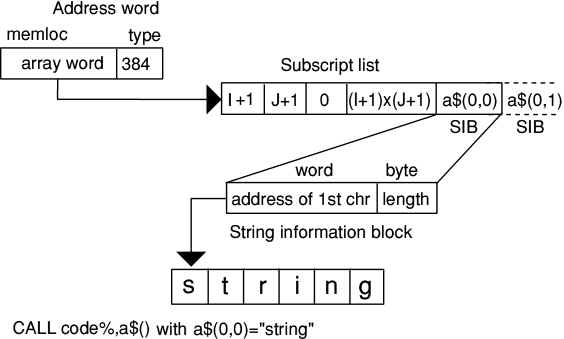
String array a$()
This is modified slightly, instead of the word long values of each element there is a 5 byte SIB block for each element as shown.
Using the template routine from part 5 we can now add the following routines to read integer and string arrays. (The full program is on the CD called parread)
.integer_array%
STMFD R13!,{R0-R5,R14} ;save required registers onto stack
MOV R5,#0 ;using R5 as a counter
BL get_no_array_elements% ;number of elements in R4 and
;R3 points to first element
.intarrayreadlp% ;start of read loop for array
LDR R0,[R3],#4 ;get element value
BL integer_to_string% ;change it to a string
BL printparamval% ;printout the value
ADD R5,R5,#1 ;add one to loop counter
CMP R5,R4 ;have reached the last value
BLT intarrayreadlp% ;if not then get next value
LDMFD R13!,{R0-R5,PC} ;restore registers and return
.string_array%
STMFD R13!,{R0-R5,R14} ;save required registers onto stack
MOV R5,#0 ;R5 used as a counter for the loop
BL get_no_array_elements% ;R4 = no and R3 points to first string SIB
.stringarraylp% ;start of the reading loop
BL get_text_from_SIB% ;load R0 with byte aligned word of SIB, R1 is length
BL printparamval% ;print out the value
ADD R3,R3,#5 ;move R3 to start of next SIB
ADD R5,R5,#1 ;add one to counter
CMP R5,R4 ;have we reached the end of the array elements?
BLT stringarraylp% ;if not then go back for next element.
LDMFD R13!,{R0-R5,PC} ;restore registers and return
These can be placed before the printparamval% subroutine.
In the readparam% routine two more conditions must be added for their types.
CMP R4,#260 ;test for integer array type 256+4
BLEQ integer_array% ;branch to its subroutine
BEQ endread%
CMP R4,#384 ;test for string array type 256+128
BLEQ string_array% ;branch to its subroutine
This code can be placed after the BEQ endread% for the direct string condition. We have now produced a routine which will read all but the real number parameters.
I will return to real numbers (floating point) in a later article.
Points to Note
- Array description blocks (address of subscript list) always start on a word boundary.
- Array values are stored in the following order (this list for an integer array created by DIM a%(1,2,3) ) a%(0,0,0) .... a%(0,0,3), a%(0,1,0) .... a%(0,1,3), a%(0,2,0) .... a%(0,2,3), a%(1,0,0) ........ a%(1,2,3) This is not the expected order. To find the address of any element (x,y,z) use the formula address=((x*dim limit)+(y*dim limit)+z)*(length of data address)+description block start address length of data address is 4 for integer arrays and 5 for strings and real number arrays.
- String array description blocks do not end on a word boundary.
Searching and Altering Array Data
The beauty of machine code routines are their speed. Most of the following can be done quite easily in BASIC but these routines will do it much quicker.
Inputting names in alphabetical order
Consider the following:
CALL input%,n$,a$()
Where n$ will contain the input name and a$() is the string array. This is often better than inputting then sorting (as it saves time).
The method is as follows:
- Check if any empty array elements if not then do nothing.
- Find the first empty array element, remember its position and load input data into its string address.
- Compare n$ with each array string until n$<= array string (remember this position)
- Move to empty element then working backwards move up each SIB block until input position reached.
- Place the empty elements string address into input position SIB block and update its length byte.
Using this method is more efficient since we only move the SIB's and not the actual data. SIBs are 5 bytes long whereas the data could be 255 chrs long. Imagine having to move the data in an array of 100 elements. This would require 25500 movements at worst if the input string needed to be inserted at the start. Moving the SIBs would require 500 movements. The annotated example is called Alphain on the CD.
While designing this routine I found a slight quirk in BASIC when assigning its memory space for string arrays. DIM a$(9) will set up the data block as described but the string addresses in each SIB element are not assigned! I suppose this saves memory, but it means we cannot write to their addresses. To get round this fill the array with single characters with a line thus:
a$()=STRING$(255,"0")
The string addresses in each SIB are assigned. Now make each array element a null string:
a$()=""
The string addresses are still assigned, only the length byte is changed to zero.
Searching data arraysOnce we have the array elements in alphabetic order we can use a binary search to find data. A binary search does not require as many comparisons as a simple search.
The Binary Search
To see how this type of search works consider the following list of data.
[Alan] [Avril] [Barry] [Brenda] [David] [Freda]
[George] [Helga] [Ian] [Jenny] [Kevin] [Kristy]
These twelve elements are in alphabetic order so a binary search can be used. Consider the search for Brenda. Set two pointers called lower and upper. Lower to point to the 1st element and upper to the last element.
- Start Search loop
- Find middle element (upper+lower)DIV 2 (integer division rounded down)
- Compare the middle element with the search string.
- Are the two strings the same?
- If so then get out of match with a flag set to true.
- If the search string less than the middle element string then make upper equal to middle.
- If the search string is greater than the middle element string then make lower equal to middle.
After the first stage the list to be considered is:
[Alan] [Avril] [Barry] [Brenda] [David] [Freda]
Now repeat the search loop and the list has now become
[Barry] [Brenda] [David] [Freda]
Repeat the search loop once more and the list is now:
[Brenda] [David] [Freda]
Repeat the search loop and the list is now:
[Brenda] [David]
After one more repeat a match is found.
If we had searched for David then everything would be the same up to the above two element list. If we do not find a match then we must check the upper element.
On the CD is the ARM code equivalent called binsearch. I have designed it to be called using:
CALL search, s$, a$(), pos%
If a match is found then pos% will contain the matching array element number. If no match then pos% equals -1. The only ARM code which needs to be explained is the MLA (multiplication with accumulate). This requires four registers, no immediate constants are allowed. The action is:
MLA R0,R1,R2,R3 R0=(R1*R2)+R3
This is useful for finding addresses of array elements since the start address can be in R3, the length of each SIB in R2 and the element number in R1.
Thats it for this time, in the next part I will be concluding the series with a look at relocatable code, floating point and the problems of 32 bit and 26 bit code.